ANALYTIC STUDY OF THERMOHALINE CONVECTIVE STABILITY IN A COUPLE-STRESS FLUID
DOI:
https://doi.org/10.22452/mjs.vol43no3.6Keywords:
Stability, energy method, Couple-stress fluid, thermohaline convection, Rayleigh numberAbstract
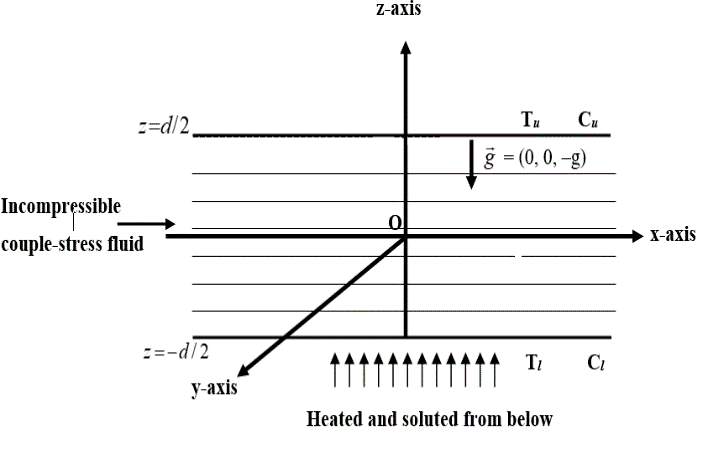
This work investigates nonlinear analysis for thermohaline convective stability in a steady, viscous, incompressible couple-stress fluid by performing a generalized energy method. It is observed that the linear and nonlinear threshold that reflects the physics of the onset of convection is the same. The couple stress and solute gradient are seen to have a stabilizing impact on the system.
Downloads
References
Chandrasekhar S. (1981) Hydrodynamic and Hydromagnetic Stability, New York, Dover.
Choudhary S. & Sunil (2019) Global stability for double-diffusive convection in a couple-stress-fluid saturating a porous medium, Studia Geotechnica et Mechanica 41(1):13. DOI: https://doi.org/10.2478/sgem-2018-0044
Galdi G. P. (1985) Nonlinear stability of the magnetic Bénard problem via a generalized energy Method, Archive of Rational Mechanics and Analysis87:167-186. DOI: https://doi.org/10.1007/BF00280699.
Galdi G. P.& Straughan B. (1985) A nonlinear analysis of the stabilizing effect of rotation in the Bénard problem, Proceedings of the Royal Society of London A. 402:257-283. DOI:10.1098/rspa.1985.0118
Galdi G. P. & Padula M. (1990) A new approach to energy theory in the stability of fluid Motion, Archive of Rational Mechanics and Analysis 110:187-286. DOI: https://doi.org/10.1007/BF00375129
Joseph D. D. (1965) On the stability of the Boussinesq equations, Archive of Rational Mechanics and Analysis20:59- 71. DOI: https://doi.org/10.1007/BF00250190.
Joseph D. D. (1966) Nonlinear stability of the Boussinesq equations by the method of energy,Archive of Rational Mechanics and Analysis 22: 163-184.DOI: https://doi.org/10.1007/BF00266474.
Joseph D. D. (1976) Stability of Fluid Motions, Springer Verlag, New York.Rionero S. (1968) Metodivariazionali per la stabilitfiasintotica in media in magnetoidrodinamica, Annali di Matematica Pura ed Applicata78:339-364. DOI: https://doi.org/10.1007/BF02415121.
Orr W. McF. (1907) Stability or instability of the steady motions of a perfect liquid, Proceedings of the Royal Irish Academy A. 27:9-68:69-138.
Reynolds O. (1895) On the dynamical theory of incompressible viscous fluids and the determination of the criterion, Philosophical Transactions Royal Society of London A. 186:123-164. DOI: http://dx.doi.org/10.1098/rsta.1895.0004
Rionero S. &Mulone G. (1988) A non-linear stability analysis of the magnetic Bénard problem through the Lyapunov direct method, Archive for Rational Mechanics and Analysis 103:347-368. DOI: DOI:10.1007/BF00251445
Mulone G. & Rionero S. (1989) On the nonlinear stability of the rotating Bénard problem via the Lyapunov direct method, Journal of Mathematical Analysis and Applications 144:109-127. DOI:10.1016/0022-247X (89)90362-4
Serrin J. (1959) On the stability of viscous fluid motions, Archive Rational Mechanics and Analysis3:1-13. DOI: https://doi.org/10.1007/BF00284160.
Stokes V. K. (1966) Couple stresses in fluids,Physics of Fluids9:1709.
Stokes V. K. (1984) Theories of Fluids with Microstructure, Springer, New York.
Straughan B. (2004) The Energy Method, Stability, and Nonlinear Convection, Springer Verlag, New York.
Sunil, Choudhary S. & Bharti P. K. (2013) Global stability for thermal convection in a couple-stress fluid with temperature and pressure dependent viscosity, Studia Geotechnica et Mechanica 35(3): 85-102. DOI:10.2478/sgem-2013-0032
Sunil, Choudhary S. & Mahajan A. (2014) Conditional stability for thermal convection in a rotating couple-stress fluid saturating a porous medium, Special Topics & Reviews in Porous Media 5(2):119-132. DOI: 10.1615/SpecialTopicsRevPorousMedia.v5.i2.30
Sunil, Choudhary S.& Mahajan A. (2019) Stability analysis of a couple-stress fluid saturating a porous medium with temperature and pressure dependent viscosity using a thermal non-equilibrium model,Applied Mathematics and Computation 340(1):15-30. DOI: https://doi.org/10.1016/j.amc.2018.08.025
Sunil, Devi R. & Mahajan A. (2011) Global stability for thermal convection in a couple stress fluid, International Communications in Heat and Mass Transfer 38: 938–942. DOI: https://doi.org/10.1016/j.icheatmasstransfer.2011.03.030
Downloads
Published
How to Cite
Issue
Section
License
Transfer of Copyrights
- In the event of publication of the manuscript entitled [INSERT MANUSCRIPT TITLE AND REF NO.] in the Malaysian Journal of Science, I hereby transfer copyrights of the manuscript title, abstract and contents to the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) for the full legal term of copyright and any renewals thereof throughout the world in any format, and any media for communication.
Conditions of Publication
- I hereby state that this manuscript to be published is an original work, unpublished in any form prior and I have obtained the necessary permission for the reproduction (or am the owner) of any images, illustrations, tables, charts, figures, maps, photographs and other visual materials of whom the copyrights is owned by a third party.
- This manuscript contains no statements that are contradictory to the relevant local and international laws or that infringes on the rights of others.
- I agree to indemnify the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) in the event of any claims that arise in regards to the above conditions and assume full liability on the published manuscript.
Reviewer’s Responsibilities
- Reviewers must treat the manuscripts received for reviewing process as confidential. It must not be shown or discussed with others without the authorization from the editor of MJS.
- Reviewers assigned must not have conflicts of interest with respect to the original work, the authors of the article or the research funding.
- Reviewers should judge or evaluate the manuscripts objective as possible. The feedback from the reviewers should be express clearly with supporting arguments.
- If the assigned reviewer considers themselves not able to complete the review of the manuscript, they must communicate with the editor, so that the manuscript could be sent to another suitable reviewer.
Copyright: Rights of the Author(s)
- Effective 2007, it will become the policy of the Malaysian Journal of Science (published by the Faculty of Science, University of Malaya) to obtain copyrights of all manuscripts published. This is to facilitate:
- Protection against copyright infringement of the manuscript through copyright breaches or piracy.
- Timely handling of reproduction requests from authorized third parties that are addressed directly to the Faculty of Science, University of Malaya.
- As the author, you may publish the fore-mentioned manuscript, whole or any part thereof, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given. You may produce copies of your manuscript, whole or any part thereof, for teaching purposes or to be provided, on individual basis, to fellow researchers.
- You may include the fore-mentioned manuscript, whole or any part thereof, electronically on a secure network at your affiliated institution, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- You may include the fore-mentioned manuscript, whole or any part thereof, on the World Wide Web, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- In the event that your manuscript, whole or any part thereof, has been requested to be reproduced, for any purpose or in any form approved by the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers), you will be informed. It is requested that any changes to your contact details (especially e-mail addresses) are made known.
Copyright: Role and responsibility of the Author(s)
- In the event of the manuscript to be published in the Malaysian Journal of Science contains materials copyrighted to others prior, it is the responsibility of current author(s) to obtain written permission from the copyright owner or owners.
- This written permission should be submitted with the proof-copy of the manuscript to be published in the Malaysian Journal of Science
Licensing Policy
Malaysian Journal of Science is an open-access journal that follows the Creative Commons Attribution-Non-commercial 4.0 International License (CC BY-NC 4.0)
CC BY – NC 4.0: Under this licence, the reusers to distribute, remix, alter, and build upon the content in any media or format for non-commercial purposes only, as long as proper acknowledgement is given to the authors of the original work. Please take the time to read the whole licence agreement (https://creativecommons.org/licenses/by-nc/4.0/legalcode ).





